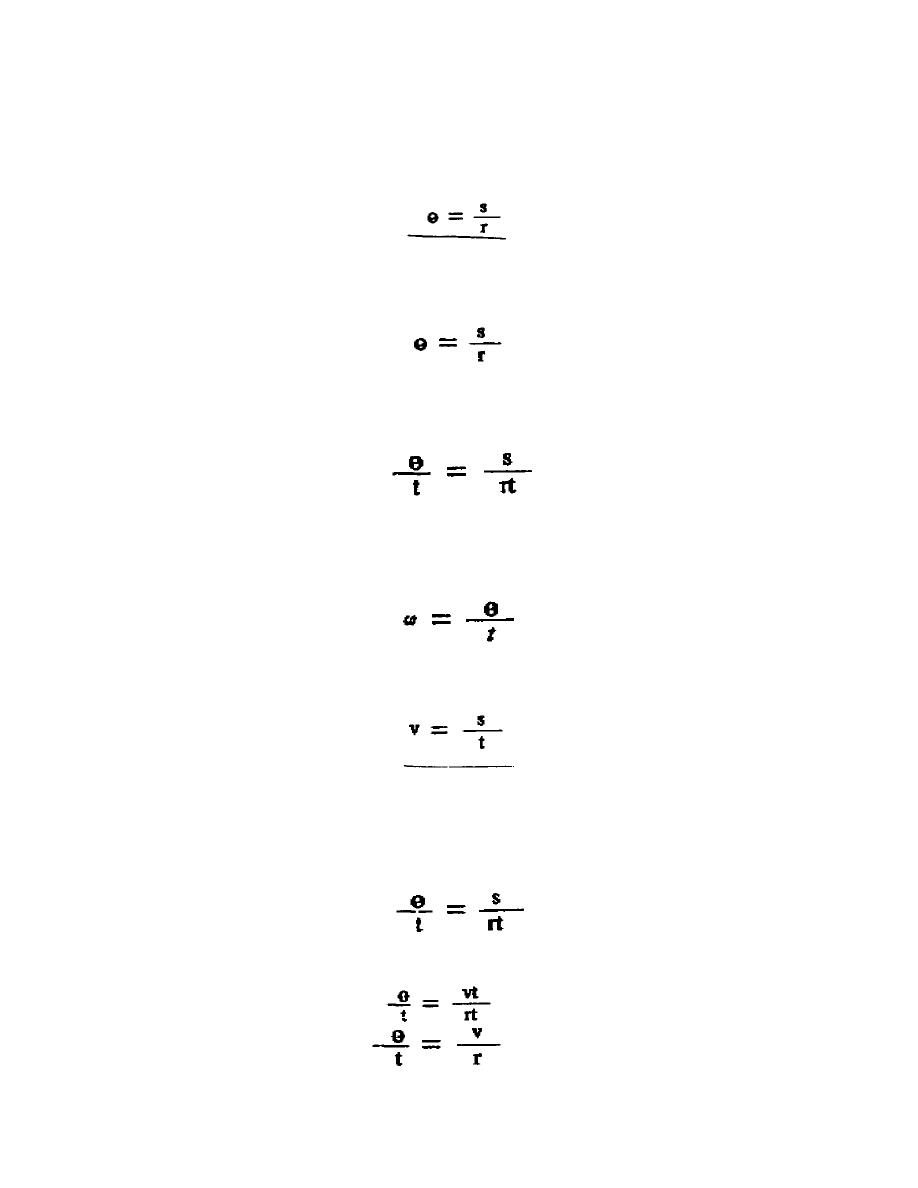
SM0486
c. Angular velocity. From Figure 2, you can see that if s were twice as long
as shown, the angle would be 2 radians, and if s were three times as long, the
angle would be e radians. Thus, the number of radians is equal to the distance, s,
on the circumference divided by the radius. Expressing this mathematically
(1) The angular velocity of rotation may also be expressed as the number of
radians per period of time; for example, the number of radians per second.
Restating the expression (1) above, which is
and applying it to a rotating vector, you have s equal to the space on the
circumference covered by the rotating vector, r equal to the length of the radius,
and equal to the number of radians. Dividing both sides by time, t, you get
(2) If t equals seconds, the left member of the equation above can be
stated as radians per second and the right member as space per second, divided by
It is common practice to let the Greek letter stand for radians per
radius.
second. Hence,
(3) Also, space or distance covered per second is velocity, which can be
represented by the letter v
(4) Solving for s in equation (4) gives
S = vt
(5) Restating (2) you have
Substituting the value of s from (5) in the right numerator gives
(6) Canceling t's gives
(7)
80


 Previous Page
Previous Page
