MM0704, Lesson 1
In any practical parallel LC circuit, there is always some resistance in the branches, mainly in the inductive branch is
the resistance of the coil winding (distributive resistance). This means that the current through the inductive branch
will lag the applied voltage by slightly less than 90. The currents through the two branches do not cancel entirely, so
there is some total current. This line current furnished by the generator is very small. A circuit that draws only a small
amount of current has a high impedance.
When the frequency of the applied voltage in a parallel circuit is such that substituting the values of L, C, and f in the
formula results in an equality, a resonant condition exists. If L, C, or f is then changed, the circuit is off resonance, the
current is increased, the impedance is decreased, the reactances are unequal, and the frequency formula is no longer
usable.
The above facts apply to parallel resonant circuits where the resistance in series with the capacitor is insignificant, and
the Q of the coil is high.
Power in the Parallel Resonant Circuit. If the circuit is known to be resonant, total power dissipated may be
calculated by
P = EI.
Whether the circuit is resonant or nonresonant, total power is equal to the sum of the power dissipated in each
resistance. Power dissipated in a circuit using a high Q coil and a condenser free of losses will be very small.
The energy lost in a parallel resonant circuit is mainly due to resistance in the windings of the coil, although, at very
high frequencies, losses also become apparent in the capacitor. Series resistance in the inductive or capacitive branch is
carefully kept to a minimum, since the smaller the series R, the smaller the I2R loss. Any resistance across the tuned
circuit (which is sometimes unavoidable) should be kept as large as possible; because the power lost is proportional to
E2/R. As with the series circuit, large losses make the resonance curve nonselective.
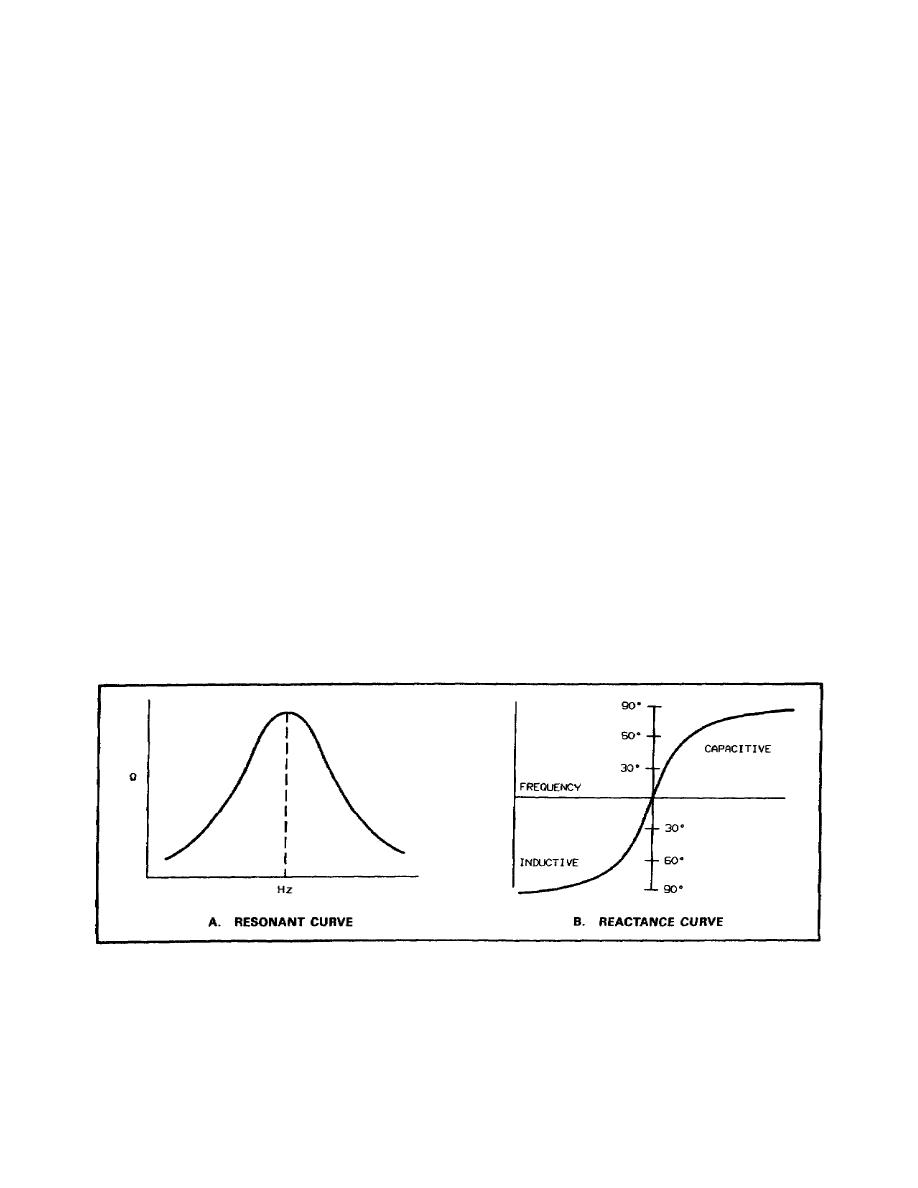
Resonance Frequency Curves. The resonant curve for the parallel circuit is shown in figure 1-8A. It is plotted for
impedance versus frequency and is similar to the current versus frequency curve of the series resonant circuit
Figure 1-8. Parallel Resonance Frequency Curves.
14




 Previous Page
Previous Page
