Figure 25.
Series-tuned circuit.
tuned circuit at resonance is the smallest possible value which the circuit
constants will permit, because the opposition to current flow from the generator is
the smallest value at resonance.
Thus we say the impedance of a series-resonant
circuit is minimum at resonance.
b. The voltage drop across the inductor and the capacitor can be many times
the applied voltage, because E = I x X.
This increase in voltage is sometimes
called the resonant rise of voltage, since the rise is greatest at resonance.
c. At frequencies below resonance, the capacitive reactance predominates and
the circuit acts like a capacitor in series with a resistor. At frequencies above
resonance, the inductive reactance predominates and the circuit behaves like an
inductor in series with a resistor.
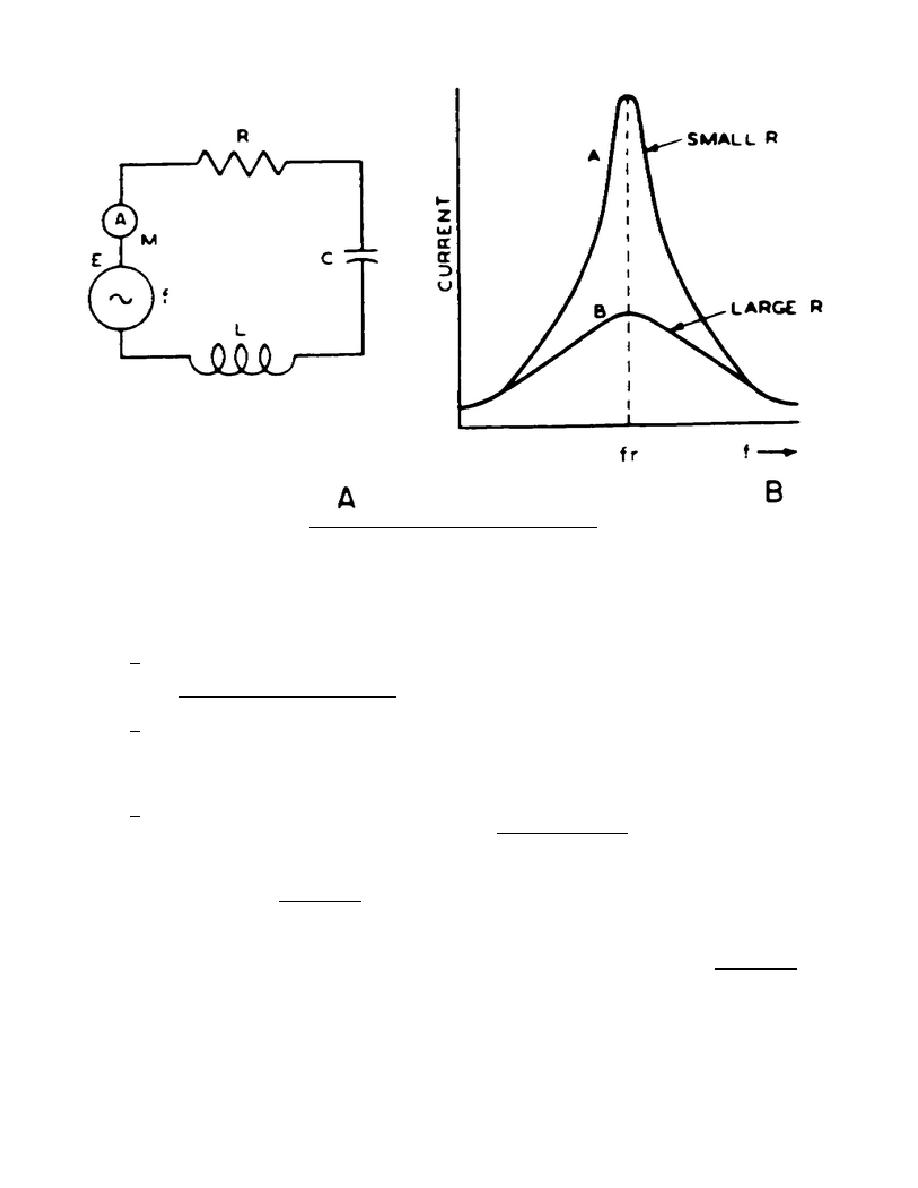
d. If the graph of line current is plotted against frequency, as in B of
figure 25, the resultant curve is called a response curve.
In a tuned circuit
having a small resistance value, the current rises sharply near the resonant
frequency (fr), whereas a large circuit resistance produces a curve that is
relatively broad and flat.
The circuit represented by curve A of the figure is
said to be much more selective, or have more selectivity than that represented by
curve B. This circuit can sharply discriminate against frequencies on either side
of resonance.
The height of the peak of the curve indicates the ability of the
tuned circuit to produce an output voltage across either the inductance or
capacitance. The circuit represented by curve A is said to be more sensitive, or
have more sensitivity than that represented by curve B.
Selectivity and
sensitivity are two important characteristics of tuned-circuits.
308
33




 Previous Page
Previous Page
