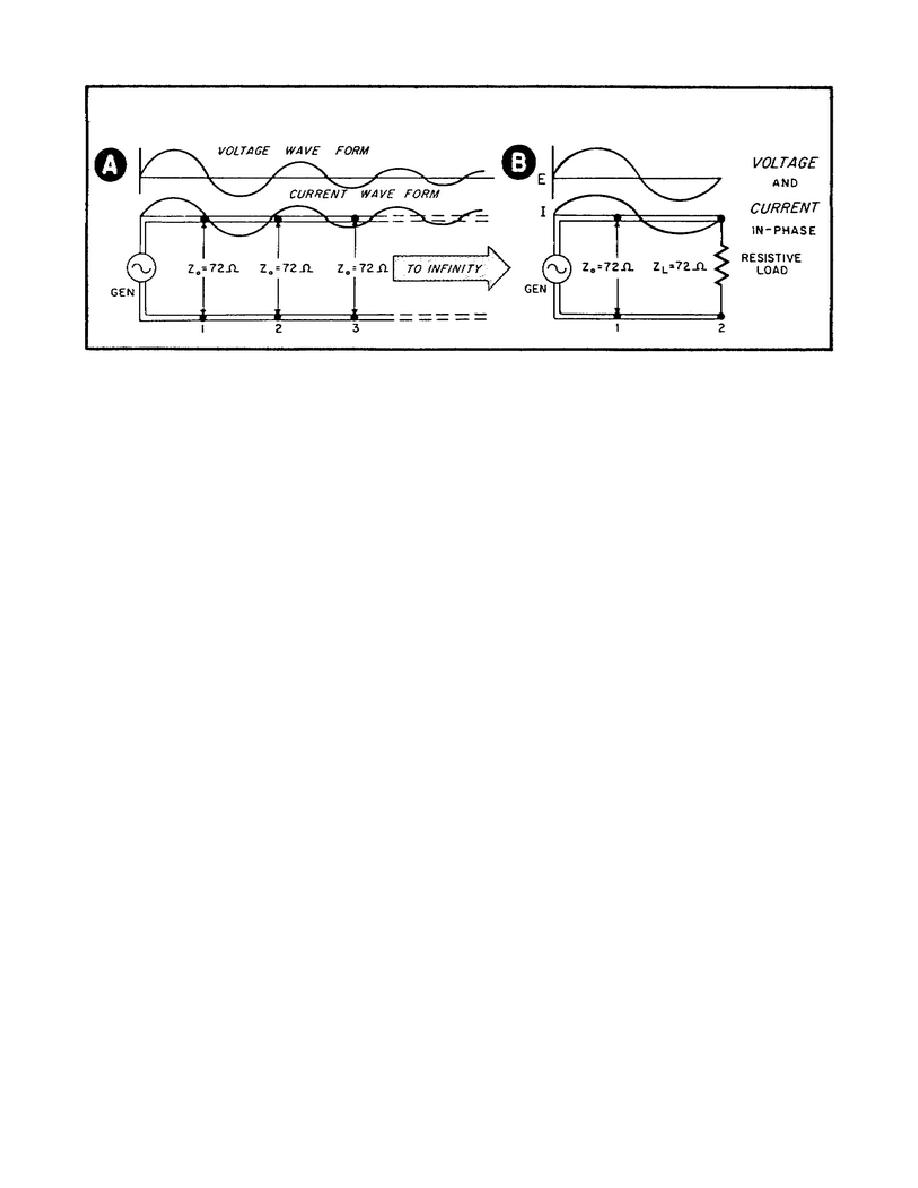
Figure 8.
The Infinitely Long Line.
15. A properly terminated line acts like an infinite line.
a. By now you are probably wondering why all this discussion regarding
an infinite line, when no such line exists. You are right, but we do have a
line that acts like an infinite line.
b. Suppose we remove a section from the infinite line between points 1
and 2. How does this affect the characteristic impedance of the line? It
doesn't.
The length of the line from point 2 on is still infinite.
Now
let's take this section of line and connect a resistive load equal to the
characteristic impedance at point 2.
See B of Figure 8.
Assume that Zo
equals 72 ohms. As far as the input is concerned, the impedance at point 2
is still equal to 72 ohms (Zo), just as if the line had extended out to
infinity. By terminating the line in a resistive load equal to Zo (72 ohms)
of the line, we have made the real line appear infinite. The voltage and
current go down the line in phase.
And what is more important, all the
energy placed on the line is absorbed by the load. We can say, then, that a
transmission line presents its characteristic impedance at its input when
the line is terminated by a load equal to the line's characteristic
impedance. Maximum power transfer occurs. That is why the characteristic
impedance of a line is so important.
16. The main points so far.
a. Terminating a line with a resistive load equal to the characteristic
impedance of the line makes the line act like an infinite line.
The
terminated line then behaves as follows:
(1) The input impedance is equal to Zo (the characteristic impedance)
and is resistive.
(2) Voltage and current travel down the line in phase.
10




 Previous Page
Previous Page
