MM0704, Lesson 1
At first, it may seem impossible that such high voltages can exist across the coil and across the capacitor with only a
small voltage applied. It is true, however, that such an increase in voltage can be obtained. The voltage across either
reactance in this case is 40 times as great as the applied voltage, a voltage gain of 40. The voltage gain of any series
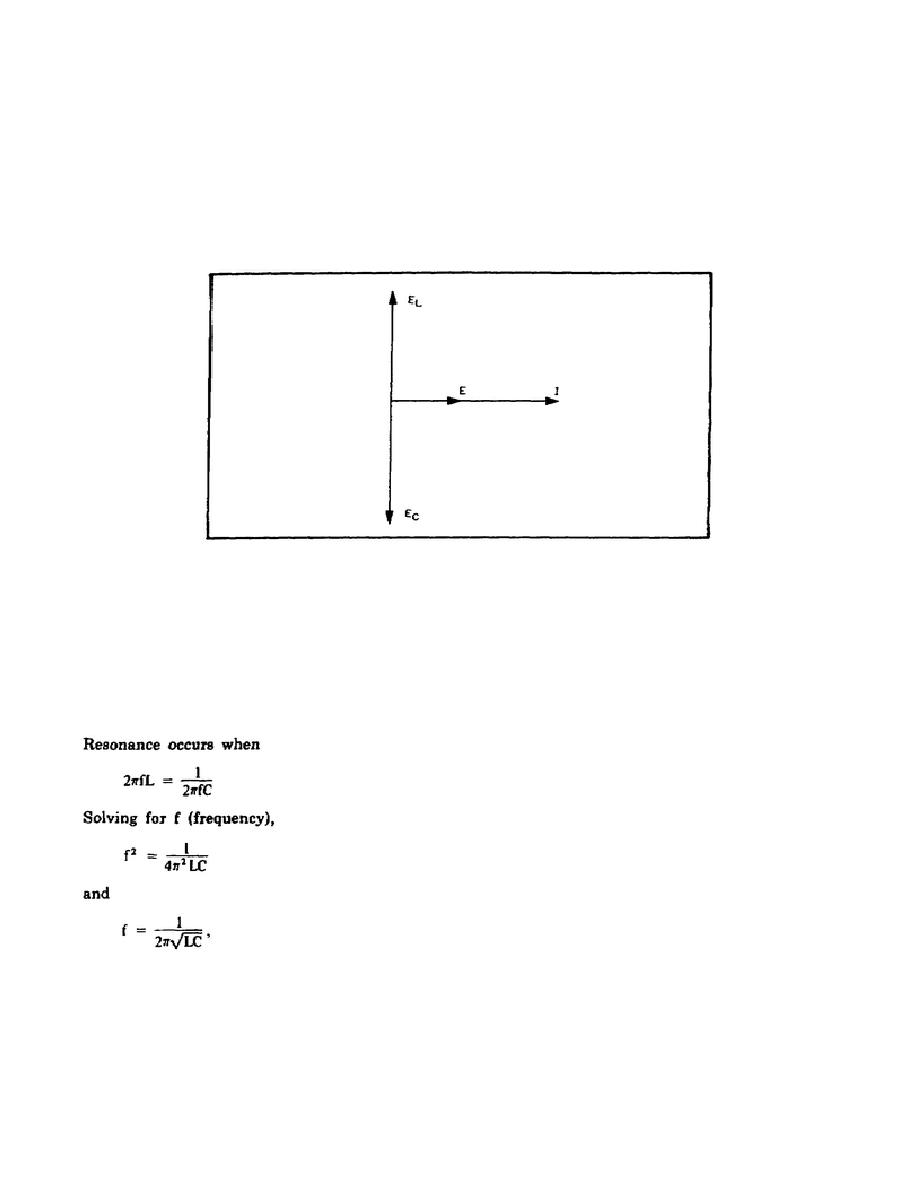
resonant circuit is the ratio of the voltage across the coil (or condenser) to the applied voltage. Figure 1-2 shows a
vector representation of this resonant circuit. Since EL leads the applied voltage by 90, and EC lags the applied
voltage by 90, these two equal voltages are 180 out of phase with each other. (Recall E is EMF.) When added
vectorially, they cancel. This means that the voltage across the series combination of the coil and capacitor is zero.
Figure 1-2. Vector Diagram of a Series Resonant Circuit.
Resonant Frequency Formula. For fixed values of L and C, there is only one frequency at which XL equals XC.
This is true because XC falls with an increase in frequency, while XL rises with an increase in frequency. Figure 1-3
shows that their values can be numerically equal at only one point, which is the point at which the lines cross. Since
the requirement for resonance is
XL = XC.
which is the equation for frequency of resonance. All quantities in the equation are in basic units: Hertz, henrys, and
farads.
9




 Previous Page
Previous Page
