2.
CONCEPTS OF ERROR ANALYSIS.
a. Measurements of any nature have errors associated with them, causing
some degree of uncertainty in the resulting data.
Unfortunately, the
usefulness of a measurement is dependent upon the accuracy of that
measurement or its closeness to the true value, which necessarily is
unknown.
The purpose of an error analysis is to estimate the bounds
(reasonable limits) of the inaccuracies of the measurement at some arbitrary
level of confidence.
Basic to any error analysis is the idea that a
measurement is the result of data-taking (known as the measurement process).
This process inevitably generates errors, resulting in an inexact
measurement.
You should analyze the process by which the measurement was
made.
b. This inexactness, or uncertainty of the measurement process
typically has two components: systematic error and random error. (Another
type of error that will be addressed later in this lesson is the gross
error, or the error created by the operator.) Systematic error usually can
only be estimated and does not follow the laws of probability.
It is
similar to misalined sights on a rifle where any shot group, no matter how
tight, would be off the bull's eye by the amount of this systematic error.
The systematic error in this case, however, is measurable in both magnitude
and direction upon looking at the target.
With a true systematic error,
neither of these attributes is known. If the magnitude and direction of the
systematic error can be determined, it becomes a correction and is then no
longer a systematic error.
In calibration systems there are usually
systematic errors that cannot be measured in magnitude or in direction.
Random error, in contrast, follows the laws of probability and can be
analyzed by statistical methods.
In the above example, random error
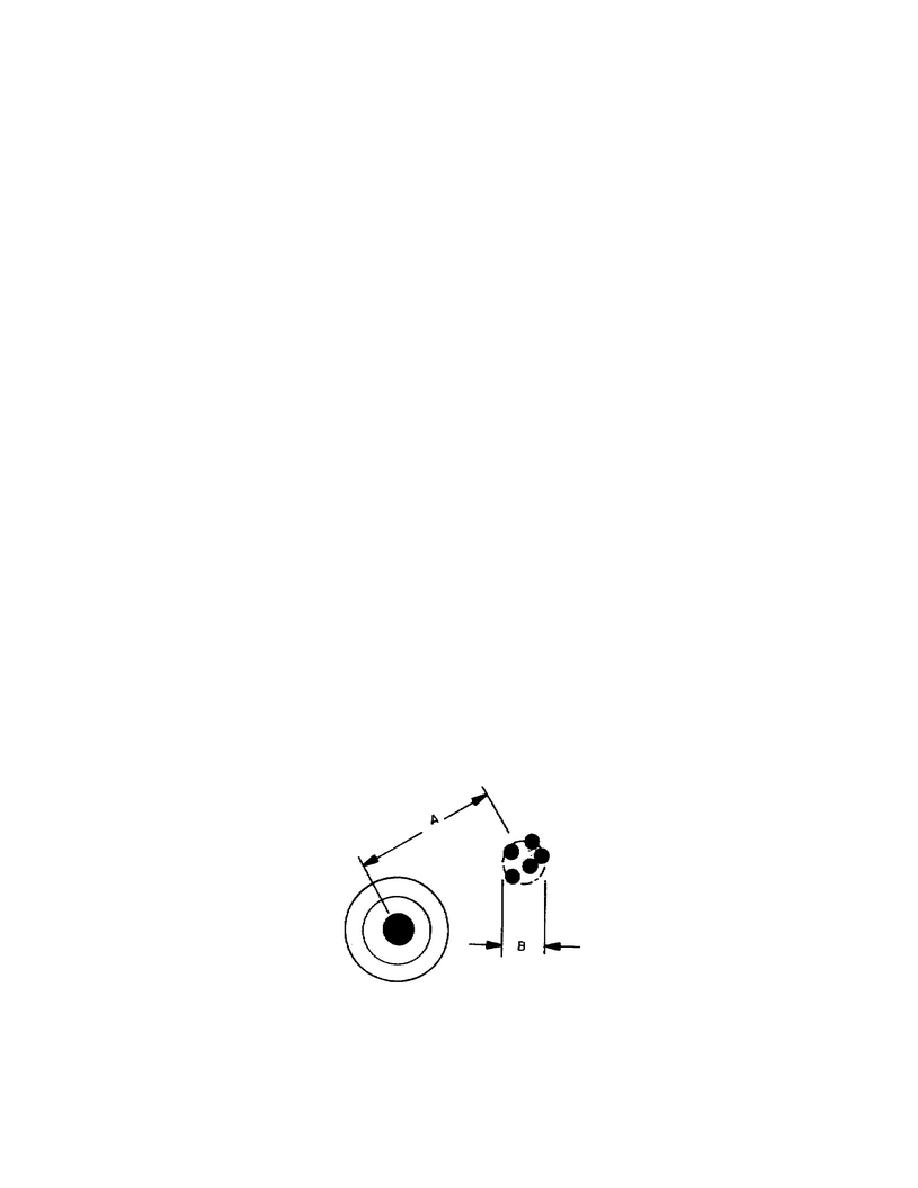
(impression) is similar to the dispersion of the shot pattern. Figure 1 is
a pattern of five shots on a target by a rifle with misalined sights.
Distance A would be a systematic error in the shooting process, if there
were no target to show the magnitude (2 inches) and the direction 5.0 from
the vertical of the misalinement.
The circle B is an indication of the
random error of the process - in this case it encloses 100% of a very small
sample of shots.
Figure 1.
Shot pattern
137



 Previous Page
Previous Page
