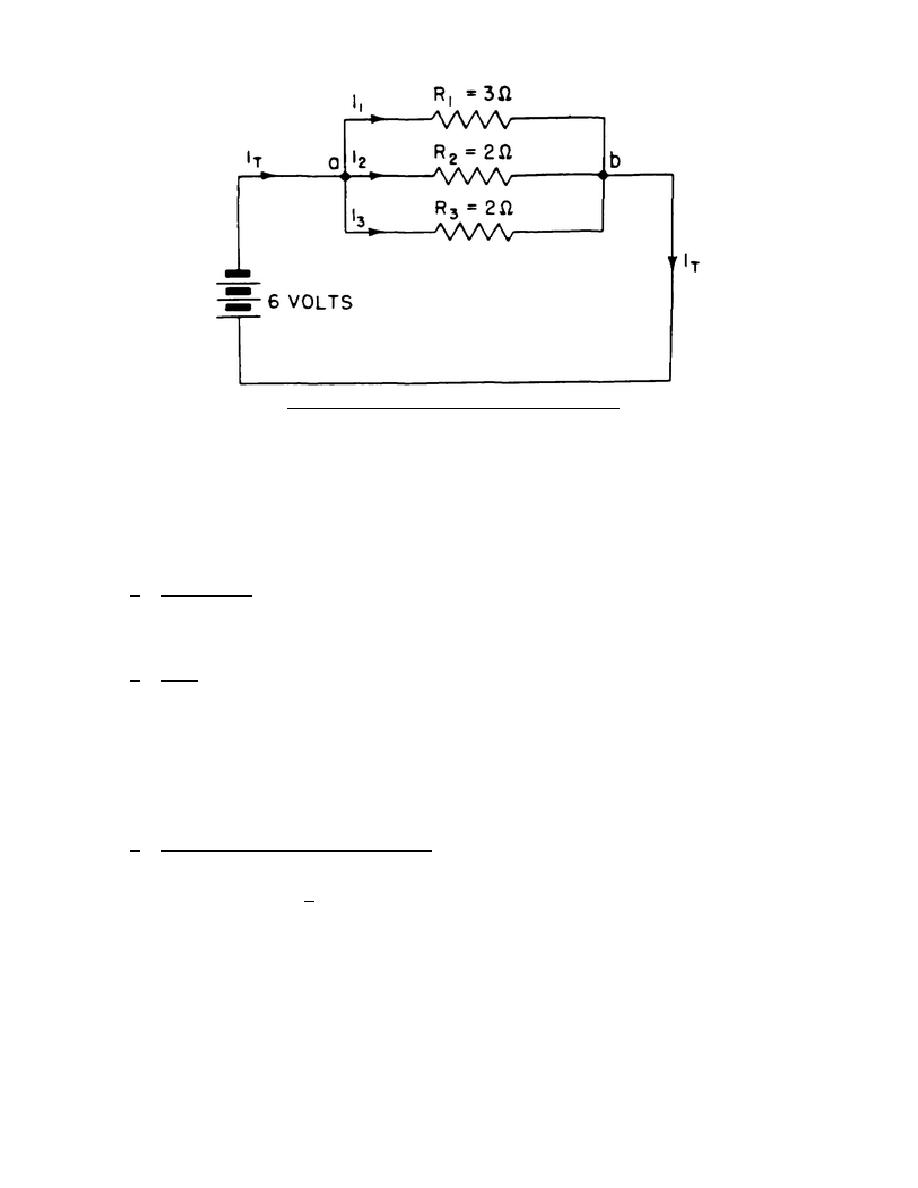
Figure 5.
Parallel-resistive circuit.
value plus that of the added path. In figure 5, if only R1 is connected to the 6-
volt source, it is known by Ohm's law (I = E/R) that the current is 6/3, or 2
amperes. When R2 is added, the same voltage is applied to it as was applied to R1.
The current through R2 must equal 6/2, or 3 amperes.
The total current from the
source is now 2 plus 3, or 5 amperes. When R3 is added, the total current from the
battery will be increased another 3 amperes or will equal 2 plus 3 plus 3, or 8
amperes. The greater the number of branches in a parallel circuit, the greater is
the current flow from the source.
c. Resistance.
Since the total current in the circuit and the applied
voltage are both known, the combined resistance of R1, R2, and R3 may be
calculated: R = E/I = 6/8, or 0.75 ohm. Note that the combined resistance is less
than the smallest value of any one resistor in the parallel combination.
d. Laws.
The three important laws relating to parallel circuits are:
(1) In a parallel circuit the same voltage is applied across each element.
(2) The total current in a parallel circuit is equal to the sum of the
currents flowing in the individual branches.
(3) The combined, or total, resistance of a parallel circuit is equal to
the applied voltage divided by the total current.
e. Combining Parallel Resistances.
(1) One method of determining the total resistance of a parallel circuit
was shown in c above. This method is satisfactory, provided the
308
9



 Previous Page
Previous Page
