as such, has played a very important part in electrical measurements. It
has fulfilled the requirements of a reference standard in a highly
satisfactory way.
4.
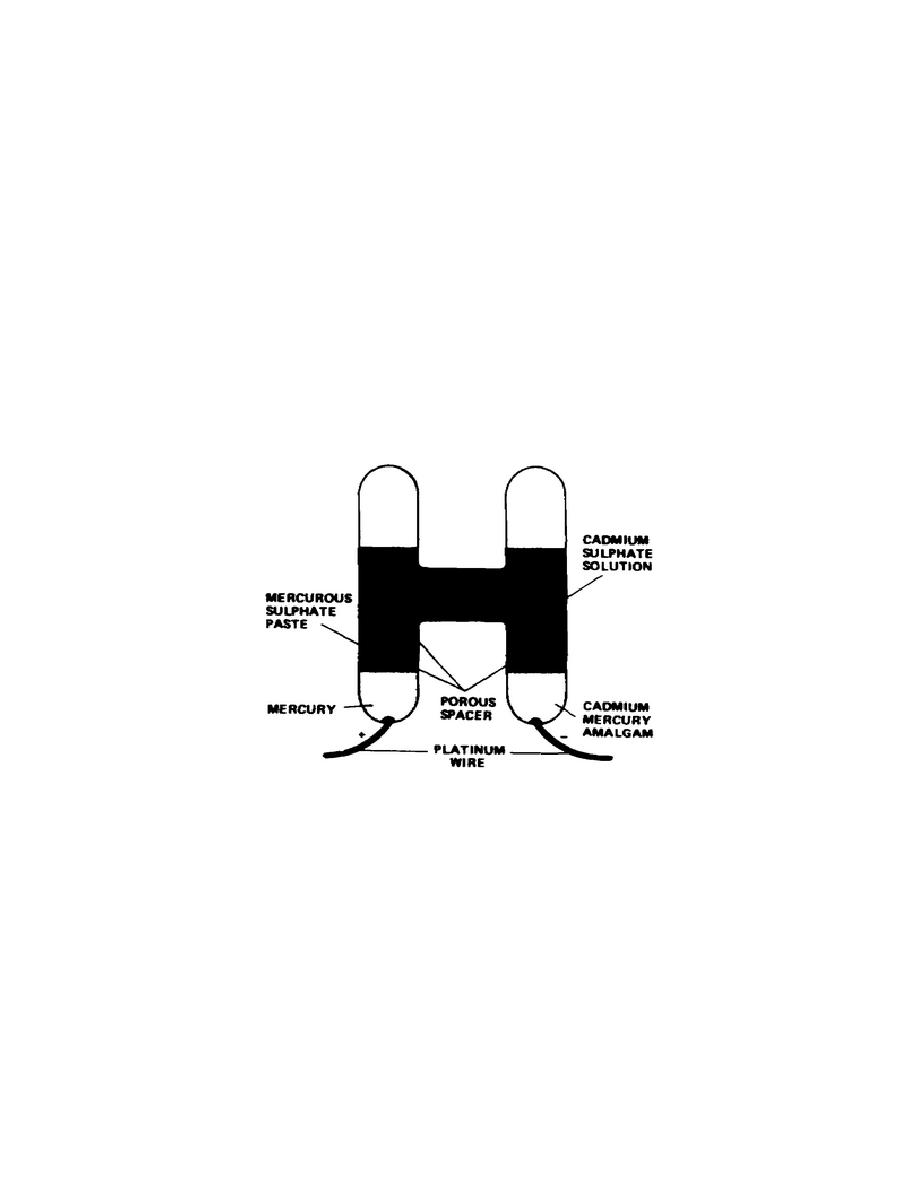
Cadmium cell. The cadmium cell is an H-shaped glass tube constructed
as shown in Figure 3-1.
The two legs of the cell have a rather high-
temperature coefficient, but the coefficient of each leg is nearly equal in
magnitude and opposite in sign. As long as the temperature of both legs is
the same, it is possible to have some variation in the ambient temperature
and still be within the tolerance of the cell. If there is a difference of
2.7C between the two legs, the EMF will be changed by 1000 microvolts or
0.1 percent. Historically, the cell was enclosed in a copper-lined case to
make sure that the temperature of both legs was approximately the same.
Even though the copper-lined case did a good job of distributing the heat
equally on both legs, it was still necessary to keep the cell out of
sunlight or other radiant heat, out of drafts of cool or warm air, and away
from either a warm or cool wall, because any of these conditions could cause
an unequal temperature on the two legs.
Modern cells are normally
maintained in a temperature-controlled oven.
Figure 3-1.
Unsaturated cell
5.
Standard cells.
The positive electrode is composed of mercury with
dipolarized mercurous sulfate paste.
The negative terminal is cadmium-
mercury amalgam and the solution is cadmium sulfate (CdSO4). There are two
types of standard cells, the saturated cell and the unsaturated cell.
Physically, the main difference between the two is that the cadmium sulphate
solution, which serves as the electrolyte, is saturated with crystals of
cadmium sulphate in the saturated cell.
In the unsaturated cell, the
electrolyte contains no crystalline formation if the temperature is kept
above 4C.
53


 Previous Page
Previous Page
