MM0704, Lesson 4
Coefficient of Coupling
The amount of coupling between the primary and secondary has a direct bearing on the mutual inductance. Coupling is
indicated by the percentage of lines of force set by the primary that cut the secondary. If 80 percent of the lines set up
by the primary cut the secondary, there is 80 percent coupling, or a coefficient of coupling of 0.8. Since mutual
inductance is directly proportional to the coefficient of coupling, the general formula for mutual inductance is
where K is the coefficient of coupling.
Example:
What is the mutual inductance of a transformer whose primary has 16 h of inductance and whose secondary has 4
h, if the coupling between the two coils is 75 percent?
Solution:
The mutual inductance of the transformer is 6 h. From the study of inductance, you learned that if two coils (L1
and L2) were connected in series, the total inductance would be Lt = L1 + L2, providing there was no effect of
coupling between the two coils. Since there usually is, the effect of coupling can be shown by an explanation of
mutual inductance.
If the series coils are close enough, there will be the mutual inductance of the first coil on the second coil and also the
mutual inductance effect of the second coil on the first. If the coils are connected in such a way that their fields add,
they are said to be series aiding. In such a case, the total inductance is:
Lt = L1 + L2 + 2M.
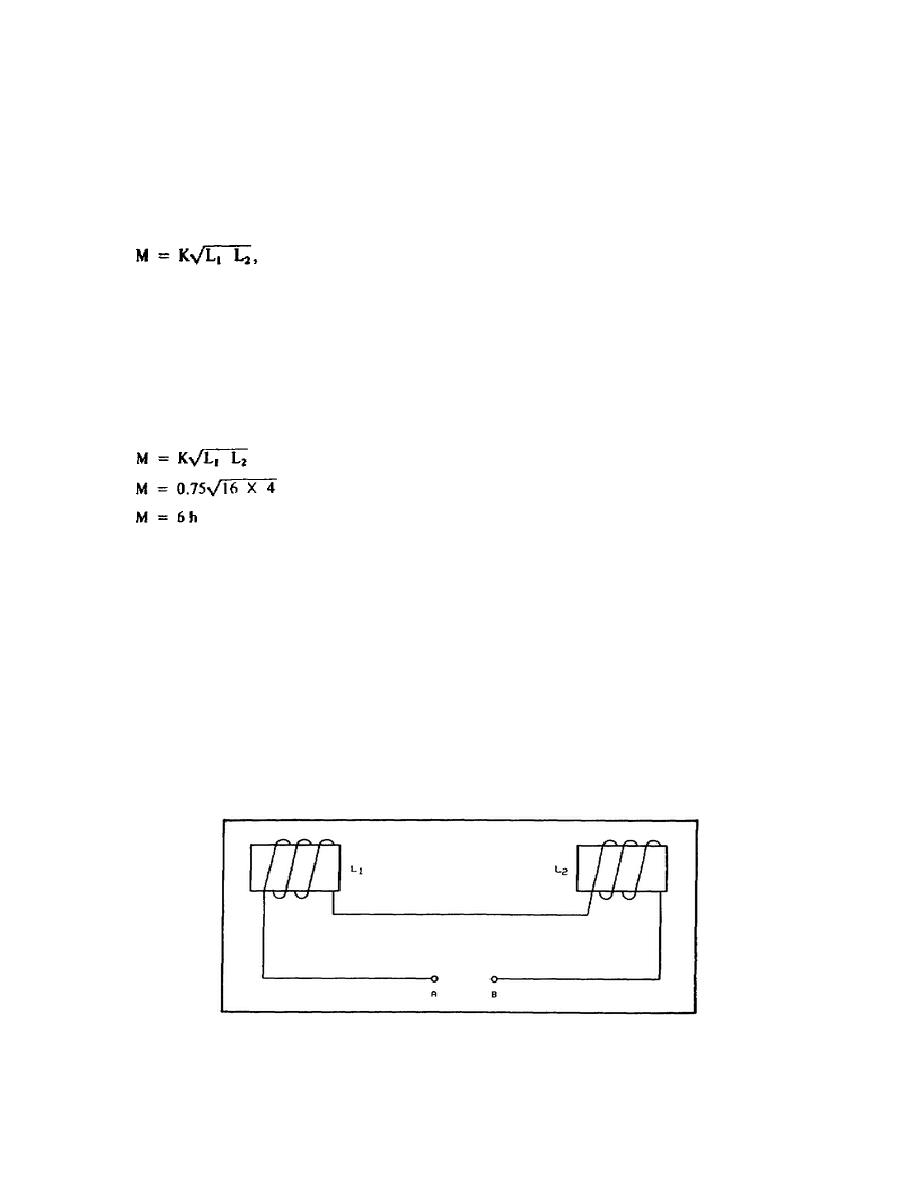
To illustrate that formula, connect the transformer of the last example as shown in figure 4-10. L1 in the problem was
16 h and L2 was 4 h. The mu-
Figure 4-10. Series Aiding Mutual Inductance.
87




 Previous Page
Previous Page
